C Program to Generate Fibonacci Series

Overview:

In this article, I will teach you how to generate the Fibonacci Series in C programming language. The n^th term of the series is obtained by adding the previous two terms of the series. The starting two terms of the series are 0 and 1. Before going to write the c program to generate Fibonacci Series, let's understand What is Fibonacci Series?, How to generate Fibonacci Series?, and What is the working principle of the Fibonacci Series? Furthermore, I will demonstrate the logic to generate the Fibonacci Series. After all, I will write logic and C Program to generate Fibonacci Series with output.

Table of contents:

1. What is Fibonacci Series?
2. How to Generate Fibonacci Series?
3. What is the working principle of the Fibonacci Series?
4. Demonstration to Generate Fibonacci Series
5. Logic to Generate Fibonacci Series
6. C Program to Generate Fibonacci Series with output
7. Conclusion

What is The Fibonacci Series?

Fibonacci Series is a series of numbers in which each number (Fibonacci number) is the sum of the two preceding numbers. The simplest form of the Fibonacci series is 1, 1, 2, 3, 5, 8, etc.

How to Generate Fibonacci Series?

Fibonacci Series generates subsequent numbers by adding two previous numbers.

Fibonacci series starts from two numbers − F0 & F1.

The initial values of F0 & F1 can be taken 0, 1 or 1, 1 respectively.

Fibonacci series satisfies the following conditions − Fn = Fn-1 + Fn-2

So a Fibonacci series can look like this − F8 = 0 1 1 2 3 5 8 13 or, this − F8 = 1 1 2 3 5 8 13 21

What is the working principle of the Fibonacci Series?

The Fibonacci series or sequence works on the principle in which each term is the sum of previous two terms”. Therefore, two sequent terms are added to generate a new term. The process continues till the last term of the series is obtained. Fibonacci Series is a set of numbers that starts with a one or a zero, followed by a one, and proceeds based on the rule that each number (called a Fibonacci number) is equal to the sum of the preceding two numbers.

Demonstration to Generate Fibonacci Series

The n^th term   known as Fibonacci number of fibonacci series is calculated by following formula:

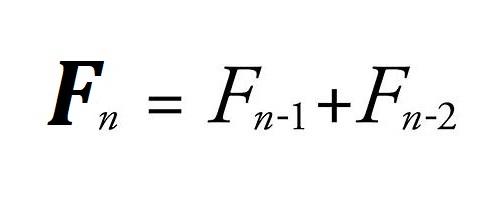
Logic to Generate Fibonacci Series

• Step 1: Take integer variable A, B, C
• Step 2: Set A = 0, B = 1
• Step 3: DISPLAY A, B
• Step 4: C = A + B
• Step 5: DISPLAY C
• Step 6: Set A = B, B = C
• Step 7: REPEAT from Step 4 to Step 6, for n times

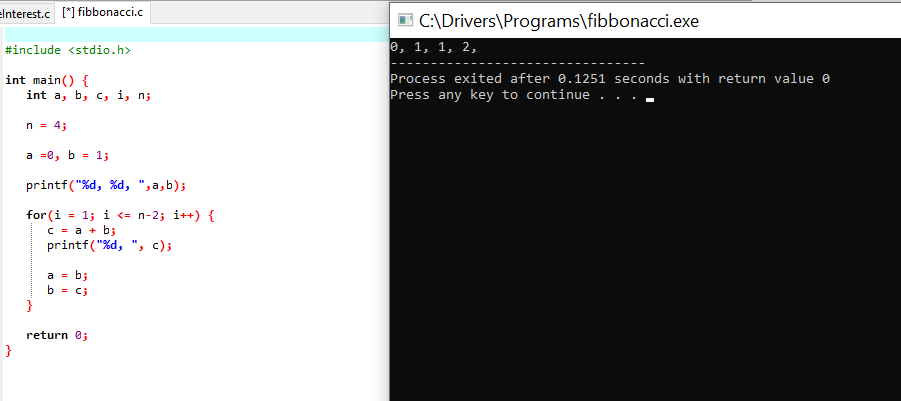
C Program to Generate Fibonacci Series with output

#include <stdio.h>

int main() {
   int a, b, c, i, n;

   n = 4;

   a =0, b = 1;
   
   printf("%d, %d, ",a,b);

   for(i = 1; i <= n-2; i++) {
      c = a + b;
      printf("%d, ", c);
      
      a = b;
      b = c;
   }
   
   return 0;
}

The output of the Program with code:

When the above code is executed, it produces the following results:

0, 1, 1, 2, 3

Conclusion:

In this Program, The first two elements are respectively started from 0, 1, and the other numbers in the series are generated by adding the last two numbers of the series using looping. These numbers are stored in an array and printed as output.