Overview:
Matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns. In this article I will introduce you with the mathematical concept Matrix and transpose of a matrix. After that, I will explain What is an array? and What is Multidimensional Array? Moreover, I will show Demonstration to Find Transpose of a Matrix. At last, I will show a C Program to Find Transpose of a Matrix with output in front of you.
Table of contents:
- What is Matrix?
- What is Transpose of a Matrix?
- What is an Array?
- What is multi dimensional array?
- Demonstration to Find Transpose of a Matrix
- Logic to Find Transpose of a Matrix
- C Program to Find Transpose of a Matrix
- Conclusion
What is Matrix?
A matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns. The matrix of r rows and c column is known as r X c matrix. Matrices are often denoted using capital roman letters such as A, B and C. For example,
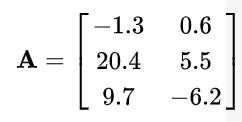
What is Transpose of a Matrix?
The transpose of a matrix can be defined as an operation on which you can switch the rows and column indices of a matrix i.e. it flips a matrix over its diagonal. To calculate the transpose of a matrix, simply interchange the rows and columns of the matrix i.e. write the elements of the rows as columns and write the elements of a column as rows. Here, the number of rows and columns in A is equal to number of columns and rows in B respectively. Thus, the matrix B is known as the Transpose of the matrix A. The transpose of matrix A is represented by A′ or AT. The following statement generalizes transpose of a matrix:
If A = [aij]m×n, then A′ =[aij]n×m.
Thus, Transpose of a Matrix is defined as “A Matrix which is formed by turning all the rows of a given matrix into columns and vice-versa.”
What is an Array?
An array is a container for the collection of items that stores these items at contiguous memory locations. An array is a variable that can store multiple values.
For example, if you want to store 100 integers in a single variable then you can create an array for it.
What is multi dimensional array?
Multidimensional array is an array of arrays. You can declare a two-dimensional (2d) array.
For example, float x[3][4];
Similarly, you can declare a three-dimensional (3d) array. For example, float y[2][4][3];
Demonstration to Find Transpose of a Matrix
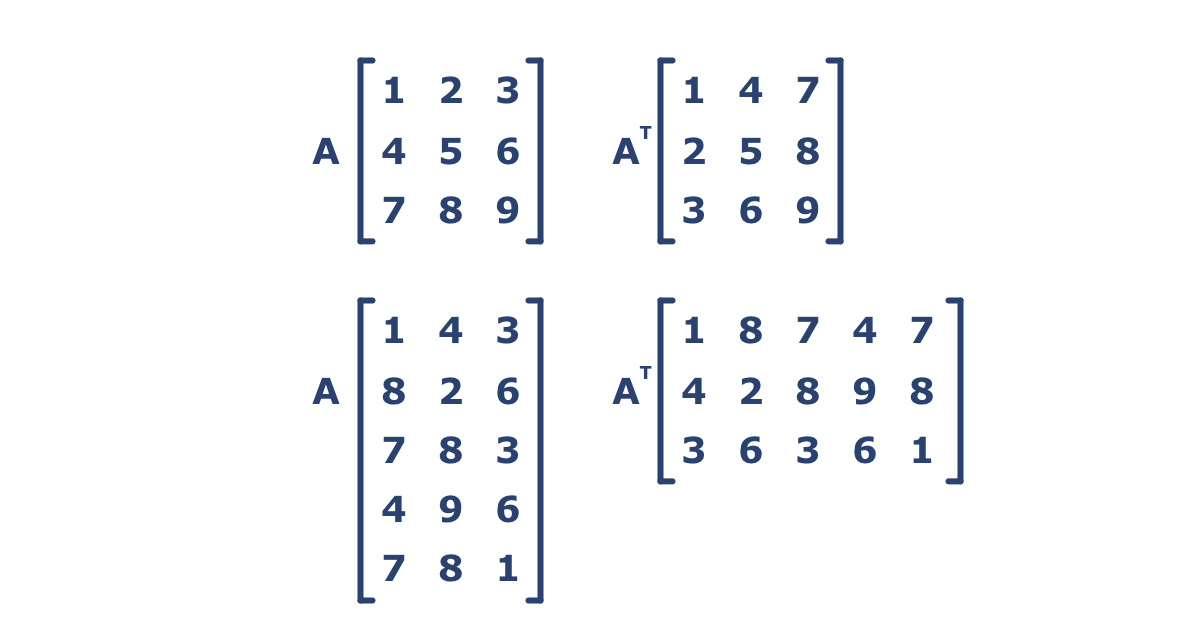
Logic to Find Transpose of a Matrix
- Take input a[][] and store elements in a{3,5,8}{3,9,0}
- Take input ‘row’ and no of rows(row) as 2
- Take input ‘col’ and no of columns(col) as 3
- 1st iteration for(i=0;i<row;i++) i.e. for(i=0;0<2;i++) Outer loop
- 1st iteration for(j=0;j<col;j++) i.e. for(j=0;0<3;j++) Inner loop
- transpose[j][i]=mat[i][j]; i.e. transpose[0][0]=mat[0][0] i.e. transpose[0][0]=3
- 2nd iteration for(j=1;j<col;j++) i.e. for(j=1;1<3;j++) Inner loop
- transpose[j][i]=mat[i][j]; i.e. transpose[1][0]=mat[0][1] i.e. transpose[1][0]=5
- 3rd iteration for(j=2;j<col;j++) i.e. for(j=2;1<3;j++) Inner loop
- transpose[j][i]=mat[i][j]; i.e. transpose[2][0]=mat[0][2] i.e. transpose[2][0]=8
- 2nd iteration for(i=1;i<row;i++) i.e. for(i=1;1<2;i++) Outer loop
- 1st iteration for(j=0;j<col;j++) i.e. for(j=0;0<3;j++) Inner loop
- transpose[j][i]=mat[i][j]; i.e. transpose[0][1]=mat[1][0] i.e. transpose[0][1]=3
- 2nd iteration for(j=1;j<col;j++) i.e. for(j=1;1<3;j++) Inner loop
- transpose[j][i]=mat[i][j]; i.e. transpose[1][1]=mat[1][1] i.e. transpose[1][1]=9
- 2nd iteration for(j=1;j<col;j++) i.e. for(j=1;1<3;j++) Inner loop
- transpose[j][i]=mat[i][j]; i.e. transpose[2][1]=mat[1][2] i.e. transpose[2][1]=0
- Now we break out of inner loop and then outer loop.
- Hence the transpose of the matrix[3,5,8][3,9,0] is tranpose[3,3][5,9][8,0].
C Program to Find Transpose of a Matrix
#include
int main() {
int a[10][10], transpose[10][10], r, c, i, j;
printf("Enter rows and columns: ");
scanf("%d %d", &r, &c);
// Assigning elements to the matrix
printf("\nEnter matrix elements:\n");
for (i = 0; i < r; ++i)
for (j = 0; j < c; ++j) {
printf("Enter element a%d%d: ", i + 1, j + 1);
scanf("%d", &a[i][j]);
}
// Displaying the matrix a[][]
printf("\nEntered matrix: \n");
for (i = 0; i < r; ++i)
for (j = 0; j < c; ++j) {
printf("%d ", a[i][j]);
if (j == c - 1)
printf("\n");
}
// Finding the transpose of matrix a
for (i = 0; i < r; ++i)
for (j = 0; j < c; ++j) {
transpose[j][i] = a[i][j];
}
// Displaying the transpose of matrix a
printf("\nTranspose of the matrix:\n");
for (i = 0; i < c; ++i)
for (j = 0; j < r; ++j) {
printf("%d ", transpose[i][j]);
if (j == r - 1)
printf("\n");
}
return 0;
}
Output of the above Program:
When this Program successfully executed then output is shown as follows:
Enter rows and columns: 2 3
Enter matrix elements:
Enter element a11: 3
Enter element a12: 5
Enter element a13: 8
Enter element a21: 3
Enter element a22: 9
Enter element a23: 0
Entered matrix:
3 5 8
3 9 0
Transpose of the matrix:
3 3
5 9
8 0

Conclusion:
This Program computes the transpose of the matrix and prints it on the screen as simply interchange the rows and columns of the matrix.

