C Program to find Power of a Number using Recursion

Overview:

In this article We will discuss calculating the Power of a Number using Recursion. First of all I would like to explain what a number is. What do you mean by the power of a number? How to calculate the power of a number? Then, I will demonstrate how to find the power of a number. Furthermore, I would write the logic and C Program to Find the Power of a Number using Recursion with output.

Table of contents:

1. What is Number?
2. What do you mean by the power of a number?
3. How to calculate the power of a number?
4. What do you mean by Recursive function?
5. Demonstration to Find the power of a number
6. Logic to Find the Power of a Number using Recursion
7. C Program to find Power of a Number using Recursion
8. Conclusion

What is Number?

A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words.

What do you mean by the power of a number?

The power (or exponent) of a number says how many times to use the number in a multiplication.

The power of a number(base^exponent)is the base multiplied to itself exponent times.

For Example,

a^b = a x a x a .....x a(b times)

2⁴ = 2 x 2 x 2 x 2 = 16

How to calculate the power of a number?

The power of a number(baseexponent)is the base multiplied to itself exponent times. To calculate the power(exponent) of a number, you will multiplied this number to exponent times i.e. if number is n and exponent is e then,

n^e= n × n × n × n × n...(e times)

For Example,

The 3 to the power 2 = 3² = 3 × 3 = 9

The 2 to the power 4 = 2 x 2 x 2 x 2 = 16

You can say that "2 to the power 4 is 16" or "the 4th power of 2 is 16"

What do you mean by Recursive function?

A recursive function is a function of code that refers to itself for execution. A recursive function is a function that calls itself during its execution. The process may repeat several times, outputting the result and the end of each iteration. A recursive function is a function that calls itself, meaning it uses its own previous terms in calculating subsequent terms. The function Count() uses recursion to count from any number between 1 and 9, to the number 10. For example, Count(1) would return 2,3,4,5,6,7,8,9,10. Count(7) would return 8,9,10. The result could be used as a roundabout way to subtract the number from 10.

Demonstration to Find the power of a number

The mathematical definition of recursive function to find power of a number is as follows:

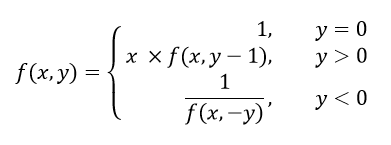This function accepts two numbers i.e. x and y and calculates x ^ y.

Let's look at this example to calculate the power of a given number:

Suppose, The number is n and its exponent is e then you will read it n to the power that looks like as follows:

n^e = n × n × n × n ...(e times)

For example, If you want to show the powers of the 23 that is calculated as follows:

23⁰ = 1

23¹ = 23

23² = 23 x 23 = 529

23³ = 23 x 23 x 23 = 12,167

23⁴ = 23 x 23 x 23 x 23 = 2,79,841

Logic to Find the Power of a Number using Recursion

The final recursive function declaration to calculate power is as follows: double power_Number(double base, int exponent);

• Step 1: First give a meaningful name to our recursive function, say power_Number().
• Step 2: The function must accept two numbers i.e. base and exponent and calculate its power.
• Step 3: Hence, take two parameters for base and exponent, say power_Number(double base, int exponent);.
• Step 4: Finally the function should return base ^ exponent i.e. a double type value.

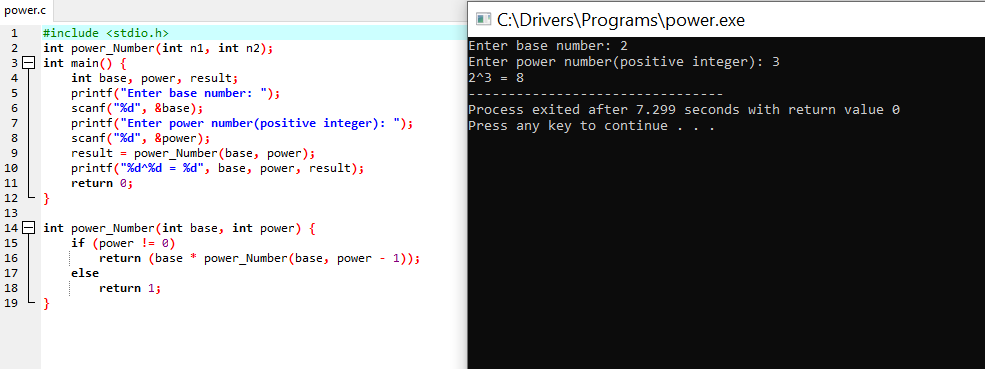
C Program to find Power of a Number using Recursion

#include <stdio.h>
int power_Number(int n1, int n2);
int main() {
    int base, power, result;
    printf("Enter base number: ");
    scanf("%d", &base);
    printf("Enter power number(positive integer): ");
    scanf("%d", &power);
    result = power_Number(base, power);
    printf("%d^%d = %d", base, power, result);
    return 0;
}

int power_Number(int base, int power) {
    if (power != 0)
        return (base * power_Number(base, power - 1));
    else
        return 1;
}

The output of the Program with code:

When the above code is executed, it produces the following results:

Enter base number: 2

Enter power number(positive integer): 3

2^3 = 8

Conclusion:

In this Program, we will solve this problem using recursion. We will first take base and exponent as input from the user and pass it to a recursive function, which will return the value of base raised to the power of exponent(base^exponent).