C program to find gcd of two numbers

Overview:

In this article, I will show you how to find the GCD of two numbers with examples and a C Program. This article include the following Table of Contents as follows:

Table of contents:

1. What is a Number?
2. What do you mean by factors?
3. What do you mean by multiple?
4. What is GCD?
5. Demonstration for GCD of two numbers
6. How to find GCD of two numbers?
7. C program to find lcm of two numbers
8. Conclusion

What is a Number?

A number is an object that uses digits to perform a mathematical task. Calculus that is a branch of mathematics included many numbers such as integers, whole numbers, real numbers, imaginary numbers so on. Here, I will discuss numbers to perform arithmetic addition operations. Moreover, a Number is a combination of digits, some symbols and decimal points. For instance, 12 and 30 are numbers.

What do you mean by factors?

Factors are numbers or quantity that when multiplied with one another produces a given number or expression.

For instance, 2, 2, and 3 are the factors of 12, and 2, 3, and 5 are the factors of 30.

What do you mean by multiple?

A multiple of a number is the product of that number and an integer. For example, 10 is a multiple of 5 because 5 × 2 = 10, so 10 is divisible by 5 and 2.

Multiple of 4 are:

4, 8, 12, 16, 20, 24, 28, 32, 36, 40.....

Multiple of 6 are:

6, 12, 18, 24, 30, 36, 42, 48......

What is GCD?

GCD (Greatest Common Divisor) or HCF (Highest Common Factor) of two numbers is the largest number that divides both of them (without a remainder). For example, the GCD of two numbers, i.e., integer 8 and 12 is 4 because, both 8 and 12 are divisible by 1, 2, and 4 (the remainder is 0), and the largest positive integer among the factors 1, 2, and 4 is 4.

Another example,

The GCD of 20 and 28 is 4.

The GCD of 98 and 56 is 14.

The Greatest Common Divisor (GCD) is also known as the Highest Common Factor (HCF), Greatest Common Factor (GCF), or Highest Common Divisor (HCD), or Greatest Common Measure (GCM).

How to find the GCD of two numbers?

• Step 1: Write the multipliers of both two numbers.
• Step 2: Take out the common between them.
• Step 3: Then to again multiply these common multipliers, Then we found the GCD of the given two numbers.

Demonstration for GCD of two numbers

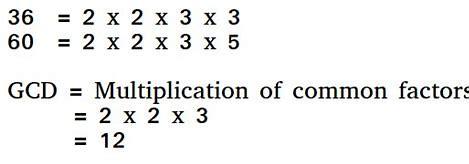
C program to find the GCD of two numbers

#include 

// Recursive function to return gcd of a and b
int gcd(int a, int b)
{
    // Everything divides 0 
    if (a == 0)
       return b;
    if (b == 0)
       return a;
  
    // base case
    if (a == b)
        return a;
  
    // a is greater
    if (a > b)
        return gcd(a-b, b);
    return gcd(a, b-a);
}
  
// Driver program to test above function
int main()
{
    int a = 98, b = 56;
    printf("%d",gcd(a, b));
    return 0;
}

The output of the Program:

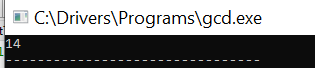
Conclusion:

This Program stores two integers one by one into the int datatype. After that find the Greatest common factor of these two numbers as shown as output.