Overview:
In this article, I will teach you how to generate the Fibonacci Series in C programming language using Recursion. Recursion means a function calling itself. The nth term of the series is obtained by adding the previous two terms of the series. The starting two terms of the series are 0 and 1. Before going to write the c program to generate Fibonacci Series, let's understand What is Fibonacci Series?, How to generate Fibonacci Series?, and What is the working principle of the Fibonacci Series? Furthermore, I will demonstrate the logic to generate the Fibonacci Series. After all, I will write logic and C Program to generate Fibonacci Series using recursion with output.
Table of contents:
- What is Fibonacci Series?
- How to Generate Fibonacci Series?
- What is Recursion?
- What is the working principle of the Fibonacci Series?
- Demonstration to Generate Fibonacci Series
- Logic to Generate Fibonacci Series
- C Program to Generate Fibonacci Series using recursion with output
- Conclusion
What is The Fibonacci Series?
Fibonacci Series is a series of numbers in which each number (Fibonacci number) is the sum of the two preceding numbers. The simplest form of the Fibonacci series is 0, 1, 1, 2, 3, 5, 8, etc.
How to Generate Fibonacci Series?
Fibonacci Series generates subsequent numbers by adding two previous numbers.
The Fibonacci series starts from two numbers: F0 & F1.
The initial values of F0 & F1 can be taken 0, 1 or 1, 1 respectively.
Fibonacci series satisfies the following conditions: Fn = Fn-1 + Fn-2
So a Fibonacci series can look like this:
F8 = 0 1 1 2 3 5 8 13
or
F8 = 1 1 2 3 5 8 13 21
What is Recursion?
Recursion means a function calling itself.
What is the working principle of the Fibonacci Series?
The Fibonacci series or sequence works on the principle in which each term is the sum of previous two terms”. Therefore, two sequent terms are added to generate a new term. The process continues till the last term of the series is obtained. Fibonacci Series is a set of numbers that starts with a one or a zero, followed by a one, and proceeds based on the rule that each number (called a Fibonacci number) is equal to the sum of the preceding two numbers.
Demonstration to Generate Fibonacci Series
The nth term known as Fibonacci number of Fibonacci series is calculated by following formula:
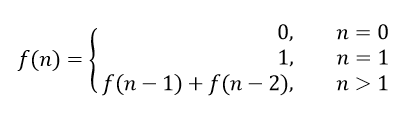

Logic to Generate Fibonacci Series
- Step 1: If
num == 0thenreturn 0. Since Fibonacci of 0th term is 0. - Step 2: If
num == 1thenreturn 1. Since Fibonacci of 1st term is 1. - Step 3: If
num > 1thenreturn fibo(num - 1) + fibo(n-2). Since Fibonacci of a term is sum of previous two terms.
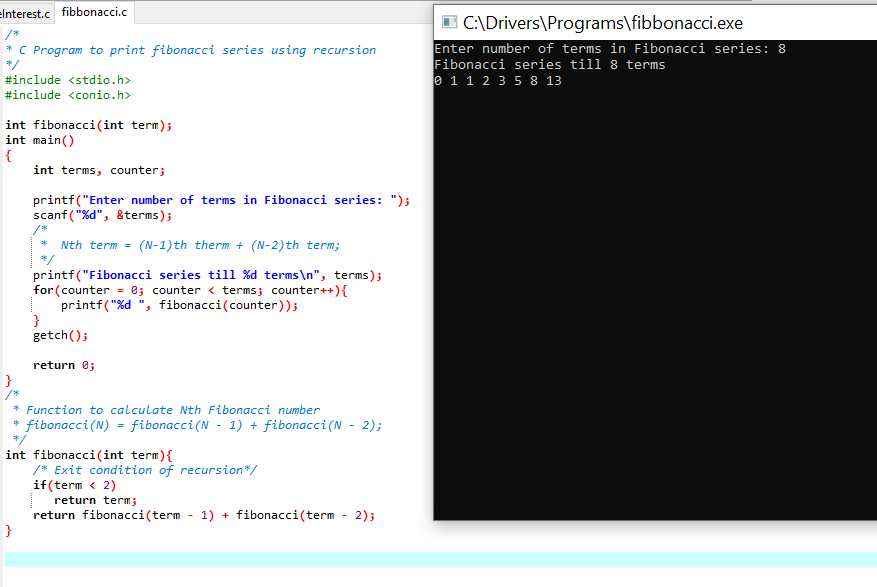
C Program to Generate Fibonacci Series using recursion with output
/*
* C Program to print fibonacci series using recursion
*/
#include <stdio.h>
#include <conio.h>
int fibonacci(int term);
int main()
{
int terms, counter;
printf("Enter number of terms in Fibonacci series: ");
scanf("%d", &terms);
/*
* Nth term = (N-1)th therm + (N-2)th term;
*/
printf("Fibonacci series till %d terms\n", terms);
for(counter = 0; counter < terms; counter++){
printf("%d ", fibonacci(counter));
}
getch();
return 0;
}
/*
* Function to calculate Nth Fibonacci number
* fibonacci(N) = fibonacci(N - 1) + fibonacci(N - 2);
*/
int fibonacci(int term){
/* Exit condition of recursion*/
if(term < 2)
return term;
return fibonacci(term - 1) + fibonacci(term - 2);
}
The output of the Program with code:
When the above code is executed, it produces the following results:
Enter number of terms in Fibonacci series: 8
Fibonacci series till 8 terms
0 1 1 2 3 5 8 13
Conclusion:
In this Program, we first takes the number of terms of Fibonacci series as input from user using scanf function. We are using a user defined recursive function named 'Fibonacci' which takes an integer(N) as input and returns the Nth Fibonacci number using recursion as discussed above. The recursion will terminate when number of terms are < 2 because we know the first two terms of Fibonacci series are 0 and 1. we are calling this function inside a for loop to get the Nth term of series.

