Overview:
In this article, We will discuss calculating the Power of a Number using Recursion. First of all, I would like to explain what a number is. What do you mean by the power of a number? How to calculate the power of a number? Then, I will demonstrate how to find the power of a number. Furthermore, I would write the logic and C Program to Find the Power of a Number using Recursion with output.
Table of contents:
- What is a Number?
- What do you mean by the factorial of a number?
- How to calculate the factorial of a number?
- What do you mean by a Recursive function?
- Logic to find factorial of a Number using Recursion
- Demonstration to find factorial of a Number using Recursion
- C Program to find factorial of a Number using Recursion
- Conclusion
What is Number?
Number is an object that uses digits to perform mathematical tasks. Calculus, which is a branch of mathematics, includes many numbers such as integers, whole numbers, real numbers, and imaginary numbers. Here, I will discuss numbers to perform arithmetic addition operations. Moreover, a Number is a combination of digits, some symbols, and decimal points. For instance, 127.23 is a rational number.
What do you mean by the factorial of a number?
The factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n.
The product of an integer and all the integers below it is known as the factorial of that integer.
By convention, the Factorial of 0 is 1. i.e., 0! = 1.
The Factorial of a negative number doesn't exist.
Factorial is represented by '!', so n factorial as (n!).
Also, n! = n*(n-1)*(n-2)*(n-3)...3*2*1
For example,
factorial four (4!) = 24.
Some other factorials examples are as follows:
0! = 1
1! = 1
2! = 1*2 =2
3! = 1*2*3 = 6
4! = 1*2*3*4 =24
5! = 1*2*3*4*5 = 120
How to calculate the factorial of a number?
The factorial of a positive number n is given by:
The factorial of n (n!) = 1 * 2 * 3 * 4...*n
The factorial of a negative number n is not possible.
The factorial of 0 is always 1.
- Step 1: Take variables as n.
- Step 2: Then, multiply the number with its first decrement, second decrement, third decrement so forth.
- Step 2: Follow the Step 2, until the 1.
For examples,
0! = 1
1! = 1
2! = 1*2 = 2
3! = 1*2*3 = 6
What do you mean by a Recursive function?
A recursive function is a function of code that refers to itself for execution. A recursive function is a function that calls itself during its execution. The process may repeat several times, outputting the result and the end of each iteration. A recursive function is a function that calls itself, meaning it uses its own previous terms in calculating subsequent terms. The function Count() uses recursion to count from any number between 1 and 9, to the number 10. For example, Count(1) would return 2,3,4,5,6,7,8,9,10. Count(7) would return 8,9,10. The result could be used as a roundabout way to subtract the number from 10.
Logic to find the factorial of a Number using Recursion
We ask the user to enter a positive integer number and we pass this number to a function called fact().
- Step 1: Inside fact() function
- Step 2: Inside fact() function, we check if the number is non-zero, if true, we execute the code inside if block orelse(if num is zero), then the code inside else block gets executed.
- Step 3: Inside if block, we add the factorial of (num-1) to the value of num.
- Step 4: num * fact(num – 1) and return the result to the calling function.
- Step 4: Inside else block, we simply return 1. Because the factorial of 0 is 1. So when num is 0, we return 1.
Demonstration to find the factorial of a Number using Recursion
We can calculate the factorial of any number using this relationship:
num! = num * (num – 1)!
where num is a positive integer number.
Suppose, The number is n then you will read the factorial of this number as n factorial and write it as n!.
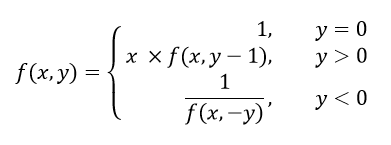 This function accepts two numbers i.e. x and y and calculates x ^ y.
This function accepts two numbers i.e. x and y and calculates x ^ y.
Let's look at this example to calculate the factorial of a number using recursion:
0! = 1 = 1
1! = 1 = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
| num | num * fact(num-1) | Iteration 1 | Iteration 2 | Iteration 3 | Iteration 4 | Iteration 5 | Result |
|---|---|---|---|---|---|---|---|
| 5 | 5 * fact(4) | 5 × 4 × fact(3) | 5 × 4 × 3 × fact(2) | 5 × 4 × 3 × 2 × fact(1) | 5 × 4 × 3 × 2 × 1 × fact(0) | 5 × 4 × 3 × 2 × 1 × 1 | 120 |
| 4 | 4 * fact(3) | 4 × 3 × fact(2) | 4 × 3 × 2 × fact(1) | 4 × 3 × 2 × 1 × fact(0) | 4 × 3 × 2 × 1 × 1 | 4 × 3 × 2 × 1 × 1 | 24 |
| 3 | 3 * fact(2) | 3 × 2 × fact(1) | 3 × 2 × 1 × fact(0) | 3 × 2 × 1 × 1 | 3 × 2 × 1 × 1 | 3 × 2 × 1 × 1 | 6 |
| 2 | 2 * fact(1) | 2 × 1 × fact(0) | 2 × 1 × 1 | 2 × 1 × 1 | 2 × 1 × 1 | 2 × 1 × 1 | 2 |
| 1 | 1 * fact(0) | 1 × 1 | 1 × 1 | 1 × 1 | 1 × 1 | 1 × 1 | 1 |
| 0 | fact(0) | 1 | 1 | 1 | 1 | 1 |
C Program to find factorial of a Number using Recursion
#include <stdio.h>
int fact(int);
int main()
{
int num;
printf("Enter a positive number to find its Factorial: ");
scanf("%d", &num);
printf("\nFactorial of %d is %d.\n", num, fact(num));
return 0;
}
int fact(int num)
{
if(num)
return(num * fact(num - 1));
else
return 1;
}
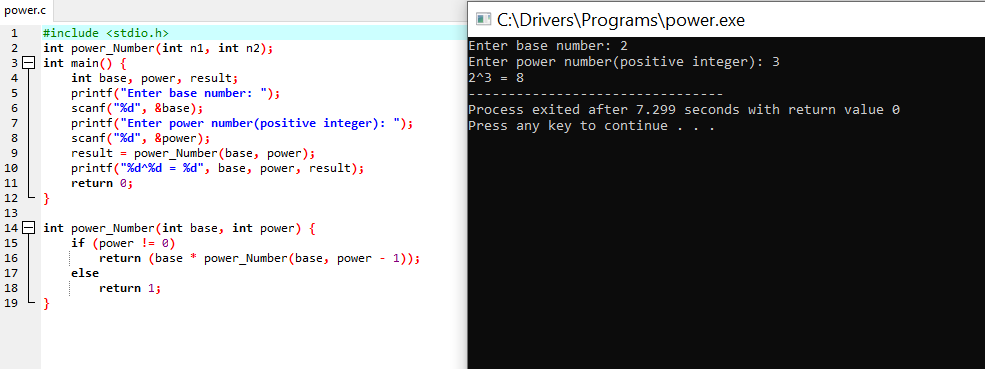
The output of the Program with code:
When the above code is executed, it produces the following results:
Enter a positive number to find its Factorial: 5
Factorial of 5 is 120.
Conclusion:
Program execution will start from the beginning of the main() function. The main function consists of fact() recursive function, this fact() function is called from main() function with user entered number n as an argument. After passing number 5 to the fact() function will call fact() function (recursive call). In recursive call, the value of that passed argument ‘n’ is decreased by 1 until n value reaches less than 1. The fact(0) will always 1. Once n value is less than one, there is no recursive call and the factorial program will calculate and print output. Your C compiler asks you to enter a number to find factorial as follows:
Enter a positive number: 5
After you enter your number, the program will be executed and give output like below:
Factorial of 5 = 120

