Overview:
In general, the term “area” is defined as the region occupied inside the boundary of a flat object or figure. Before, Starting this article First of all, I want to introduce you with Geometric Shape Trapezium . Then I will explain What do you mean by area of a Trapezium . Moreover, I will demonstrate how to find area of a Trapezium? Furthermore, I will write logic and c program to find area of Trapezium with output. After all, I will explain the resultant output.
Table of contents:
- What are the characteristics of quadrilateral?
- What is a Trapezium?
- What are the properties of the Trapezium?
- What do you mean by the area of a Trapezium?
- Demonstration how to find area of a Trapezium.
- Main Logic to find the area of a Trapezium
- C program to find area of Trapezium
- Conclusion
What are the characteristics of quadrilateral?
The word Quadrilateral is derived from the two latin words quad and lateral which means four and sides respectively. A Quadrilateral has four-sides, it is 2-dimensional (a flat shape), closed (the lines join up), and has straight sides.
What is a Trapezium ?
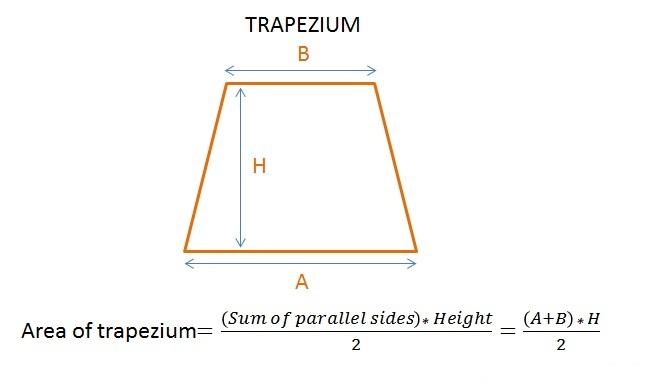
A Trapezium is a two-dimensional flat geometrical shape with four edges. A Trapezium is a type of quadrilateral with one pair of sides parallel. A Trapezium ABCD has four sides as AB, BC, CD, and DA and angles A, B, C, and D. The parallel sides are called the bases of the trapezium denoted as AB and CD and the other two sides are called it's legs denoted as AC and BD. The perpendicular distance between parallel sides is called height of trapezium denoted as h.
What are the properties of the Trapezium ?
The properties of Trapezium are given below:
- It has four edges and four vertices.
- The one pair of opposite sides is parallel.
- Area is calculated from length of parallel sides and the distance between them.
- It’s a quadrilateral with four edges.
- Sum of all interior angles equal to 360 degrees.
- The sum of the two adjacent angles of a trapezium is 180 degrees.
What do you mean by the area of a Trapezium ?
The area of trapezium depends on its parallel sides and distance between the parallel sides. If we know the length of parallel sides and the distance between them, then we can easily find the area of trapezium.
The area of a trapezium is calculated as follows:
A = [(sum of the length of the parallel edges) * height]/2
A = [(AB + CD) * h]/2
Where,
h is the distance between parallel lines of the Trapezium.
AB and CD are the parallel edges of the Trapezium.
Demonstration how to find area of a Trapezium
Main Logic to find the area of a Trapezium
The code will use 5 variables as all sides of trapezium and one for the perpendicular distance between the two parallel sides. For the area variable calculation we will take a float variable that will be initialised with the value. To calculate it we will use the formula “ ½ x (sum of length of parallel sides) x perpendicular distance between parallel sides ”.
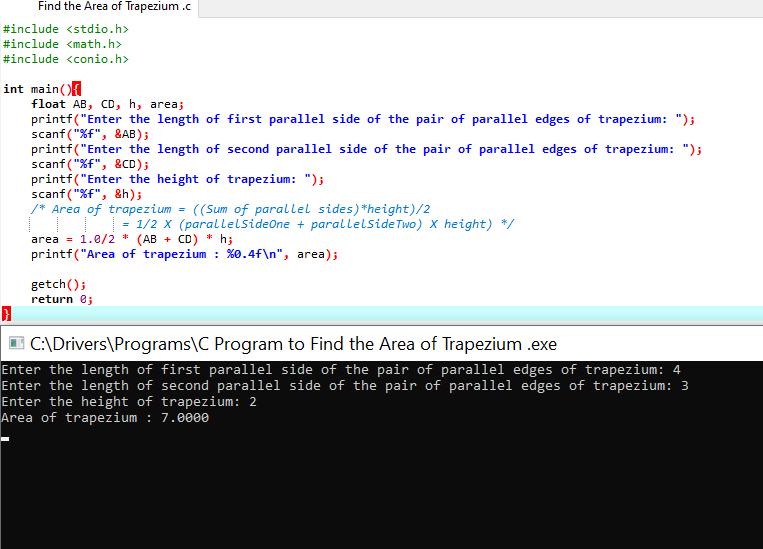
C program to find area of Trapezium
/*
* C Program to calculate area of trapezium
*/
#include <stdio.h>
#include <conio.h>
#include <math.h>
int main(){
float AB, CD, h, area;
printf("Enter the length of first parallel side of the pair of parallel edges of trapezium: ");
scanf("%f", &AB);
printf("Enter the length of second parallel side of the pair of parallel edges of trapezium: ");
scanf("%f", &CD);
printf("Enter the height of trapezium: ");
scanf("%f", &h);
/* Area of trapezium = ((Sum of parallel sides) * height)/2
= 1/2 X (AB + CD) X h) */
area = 1.0/2 * (AB + CD) * h;
printf("Area of trapezium : %0.4f\n", area);
getch();
return 0;
}
The output of the Program:
Enter the length of parallel sides of trapezium 4 7 Enter the height of trapezium 3.5 Area of trapezium : 19.2500
Conclusion
Above program first takes, length of parallel sides and height as input form user using scanf function and stores it in three floating point variables. Then it calculates the area of trapezium using the formula given above. Then, it prints the area of trapezoid on screen using printf function.

